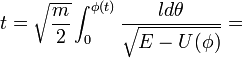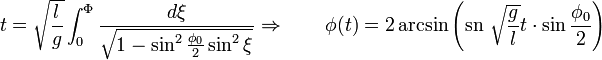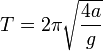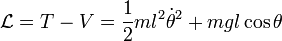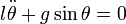Concepto de producto Pendulo o cascada
¿Que es una cascada? cepto de cascada hace referencia a las caídas de agua que se producen a una determinada altura como consecuencia de un notorio desnivel en el cauce. Cuando las cascadas poseen grandes dimensiones se las define como cataratas.
El caudal de una cascada varía según la época del año, mientras que la altura, las formas, la anchura del lecho y los tipos de paredes por los cuales cae el agua pueden depender de múltiples factores geológicos.
Cuando el agua cae desde el punto más alto de una cascada, su velocidad no es llamativa debido a que el aire genera resistencia. Este mismo motivo hace que se segmente en distintos chorros o saltos. Cabe resaltar que las cascadas pueden retroceder y desplazarse en dirección a la fuente del río cuando las rocas blandas que se acumulan en su base se desmoronan.
A nivel mundial, la caída más importante es el denominado salto Ángel, que alcanza una altura de 979 metros. Este salto surge por el avance del río Churún desde el Auyantepuy, en el estado venezolano de Bolívar.
La segunda caída más alta es el salto del Tugela, con 947 metros. Esta cascada se encuentra en la provincia de KwaZulu-Natal, en Sudáfrica.
En cuanto a la caída más ancha del mundo, se trata de las Cataratas Victoria, en la frontera entre Zambia y Zimbabwe. Su anchura es de 1,7 kilómetros.
Además de las citadas, tampoco podemos obviar a otras cascadas que, por diversos motivos, son muy afamadas en todo el mundo. Entre ellas se encuentran, por ejemplo, las cataratas del Niágara que se sitúan en la frontera entre Canadá y Estados Unidos y que han conseguido ser absolutas protagonistas en el ámbito del cine. Y es que varias son las películas que las han tomando como claves: Niágara (1953), Superman II (1980)…
Asimismo también habría que resaltar las cataratas del Iguazú, sitas entre Brasil y Argentina, que tienen el privilegio de haber sido elegidas como una de las Siete Maravillas Naturales del Mundo. En ellas sobresale, de entre sus 275 saltos, la conocida Garganta del Diablo que tiene una altura de 80 metros.
Al hablar de cascada tampoco podemos pasar por alto que bajo ese nombre también se encuentra un grupo de música alemán, de eurodance, que comenzó su andadura en el año 2004 y que ya cuenta con una serie importante de éxitos a sus espaldas destacando especialmente el que lograron con su canción “Everytime We Touch”. Yanou, Natalie Horter y DJ Manian son los tres componentes de esta formación que cuenta con diversos galardones internacionales como son los International Dance Music Awards, los World Music Awards o los MTV Video Music Awards.
De la misma forma, hay que resaltar que también se emplea el término cascada en el ámbito de la informática para referirse a un tipo de modelo de creación de software.
Cabe mencionar que, en otros contextos, la palabra cascada hace referencia a aquello que se considera gastado, está golpeado o carente de fuerza (“Aquel adorno está cascado ya que se cayó desde arriba de la mesa”).
¿Que es un pendulo?
El péndulo (del lat. pendŭlus, pendiente)1 es un sistema físico que puede oscilar bajo la acción gravitatoria u otra característica física (elasticidad, por ejemplo) y que está configurado por una masa suspendida de un punto o de un eje horizontal fijos mediante un hilo, una varilla, u otro dispositivo que sirve para medir el tiempo.
Existen muy variados tipos de péndulos que, atendiendo a su configuración y usos, reciben los nombres apropiados: péndulo simple, péndulo compuesto, péndulo cicloidal, doble péndulo, péndulo de Foucault, péndulo de Newton, péndulo balístico, péndulo de torsión, péndulo esférico, etcétera.
Sus usos son muy variados: medida del tiempo (reloj de péndulo, metrónomo, ...), medida de la intensidad de la gravedad, etc.
Péndulo simple o matemático
También llamado péndulo ideal, está constituido por un hilo inextensible de masa despreciable, sostenido por su extremo superior de un punto fijo, con una masa puntual sujeta en su extremo inferior que oscila libremente en un plano vertical fijo.
Al separar la masa pendular de su punto de equilibrio, oscila a ambos lados de dicha posición, desplazándose sobre una trayectoria circular con movimiento periódico.
Ecuación del movimiento
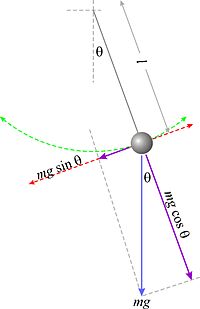
Para escribir la ecuación del movimiento, observaremos la figura adjunta, correspondiente a una posición genérica del péndulo. La flecha azul representa el peso de la masa pendular. Las flechas en color violeta representan las componentes del peso en las direcciones tangencial y normal a la trayectoria.
Aplicando la Segunda ley de Newton en la dirección del movimiento, tenemos
donde el signo negativo tiene en cuenta que la  tiene dirección opuesta a la del desplazamiento angular positivo (hacia la derecha, en la figura). Considerando la relación existente entre la aceleración tangencial y la aceleración angular
tiene dirección opuesta a la del desplazamiento angular positivo (hacia la derecha, en la figura). Considerando la relación existente entre la aceleración tangencial y la aceleración angular
obtenemos finalmente la ecuación diferencial del movimiento plano del péndulo simple
Período de oscilación
El astrónomo y físico italiano Galileo Galilei, observó que el periodo de oscilación es independiente de la amplitud, al menos para pequeñas oscilaciones. En cambio, éste depende de la longitud del hilo. El período de la oscilación de un péndulo simple restringido a oscilaciones de pequeña amplitud puede aproximarse por:
Para oscilaciones mayores la relación exacta para el período no es constante con la amplitud e involucra integrales elípticas de primera especie:
Donde φ0 es la amplitud angular máxima. La ecuación anterior puede desarrollarse en serie de Taylor obteniéndose una expresión más útil:
Solución de la ecuación de movimiento
Para amplitudes pequeñas, la oscilación puede aproximarse como combinación lineal de funciones trigonométricas. Para amplitudes grandes puede probarse el ángulo puede expresarse como combinación lineal de funciones elípticas de Jacobi. Para ver esto basta tener en cuenta que la energía constituye una integral de movimiento y usar el método de la cuadratura para integrar la ecuación de movimiento:
Donde, en la última expresión se ha usado la fórmula del ángulo doble y donde además:
-
 , es la energía, que está relacionada con la máxima amplitud
, es la energía, que está relacionada con la máxima amplitud  .
. -
 , es la energía potencial.
, es la energía potencial.
Realizando en variable  , la solución de las ecuaciones del movimiento puede expresarse como:
, la solución de las ecuaciones del movimiento puede expresarse como:
Donde:
-
 , es la función elíptica de Jacobi tipo seno.
, es la función elíptica de Jacobi tipo seno. -

El lagrangiano del sistema es 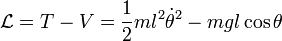 , donde
, donde  es el ángulo que forma la cuerda del péndulo a lo largo de sus oscilaciones (es la variable), y
es el ángulo que forma la cuerda del péndulo a lo largo de sus oscilaciones (es la variable), y  es la longitud de la cuerda (es la ligadura). Si se aplican las ecuaciones de Lagrange se llega a la ecuación final del movimiento:
es la longitud de la cuerda (es la ligadura). Si se aplican las ecuaciones de Lagrange se llega a la ecuación final del movimiento: 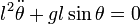 . Es decir, la masa no influye en el movimiento de un péndulo.
. Es decir, la masa no influye en el movimiento de un péndulo.
Péndulo esférico
Un péndulo esférico es un sistema con dos grados de libertad. El movimiento está confinado a la una porción de superficie esférica (de radio l) comprendida entre dos paralelos. Existen dos integrales de movimiento, la energía E y la componente del momento angular paralela al eje vertical Mz. La función lagrangiana viene dada por:
Donde  es el ángulo polar y
es el ángulo polar y  es el ángulo que forma el hilo o barra del péndulo con la vertical. Las ecuaciones de movimiento, obtenidas introduciendo el lagrangiano anterior en las ecuaciones de Euler-Lagrange son:
es el ángulo que forma el hilo o barra del péndulo con la vertical. Las ecuaciones de movimiento, obtenidas introduciendo el lagrangiano anterior en las ecuaciones de Euler-Lagrange son:
La segunda ecuación expresa la constancia de la componente Z del momento angular y por tanto lleva a la relación entre la velocidad de giro polar y el momento angular y por tanto a reescribir la lagrangiana como:
Y el problema queda reducido a un problema unidimensional.
Período
El movimiento de un péndulo esférico en general no resulta periódico, ya que es la combinación de dos movimientos periódicos de períodos generalmente incomensurables. Sin embargo el movimiento resulta cuasiperiódico, lo cual significa que fijado una posición y una velocidad previas del movimiento existe un tiempo T tal que el movimiento pasará a una distancia tan pequeña como se desee de esa posición con una velocidad tan parecida como se quiera, pero sin repetirse exactamente. Dada que la región de movimiento además resulta compacta, el conjunto de puntos la trayectoria de un péndulo esférico constituye un conjunto denso sobre una área esférica comprendida entre dos casquetes esféricos.
Solución de la ecuación de movimiento
Las ecuaciones de movimiento pueden expresarse en términos de integrales elípticas de primera especie y tercera especie:
Oscilador armónico
Se dice que un sistema cualquiera, mecánico, eléctrico, neumático, etc. es un oscilador armónico si cuando se deja en libertad, fuera de su posición de equilibrio, vuelve hacia ella describiendo oscilaciones sinusoidales, o sinusoidales amortiguadas en torno a dicha posición estable.
El ejemplo es el de una masa colgada a un resorte. Cuando se aleja la masa de su posición de reposo, el resorte ejerce sobre la masa una fuerza que es proporcional al desequilibrio (distancia a la posición de reposo) y que está dirigida hacia la posición de equilibrio. Si se suelta la masa, la fuerza del resorte acelera la masa hacia la posición de equilibrio. A medida que la masa se acerca a la posición de equilibrio y que aumenta su velocidad, la energía potencial elástica del resorte se transforma en energía cinética de la masa. Cuando la masa llega a su posición de equilibrio, la fuerza será cero, pero como la masa está en movimiento, continuará y pasará del otro lado. La fuerza se invierte y comienza a frenar la masa. La energía cinética de la masa va transformándose ahora en energía potencial del resorte hasta que la masa se para. Entonces este proceso vuelve a producirse en dirección opuesta completando una oscilación.
Si toda la energía cinética se transformase en energía potencial y viceversa, la oscilación seguiría eternamente con la misma amplitud. En la realidad, siempre hay una parte de la energía que se transforma en otra forma, debido a la viscosidad del aire o porque el resorte no es perfectamente elástico. Así pues, la amplitud del movimiento disminuirá más o menos lentamente con el paso del tiempo. Se empezará tratando el caso ideal, en el cual no hay pérdidas. Se analizará el caso unidimensional de un único oscilador (para la situación con varios osciladores, véase movimiento armónico complejo).
Péndulo cicloidal
Las oscilaciones del péndulo simple sólo son isócronas para pequeñas amplitudes. Sin embargo, existe un diseño especial en el que el período es independiente de la amplitud; se trata del péndulo cicloidal, llamado así porque está basado en una propiedad de la curva geométrica llamada cicloide.
Historia
Fue a Huygens a quien correspondió las primicias de este descubrimiento:
-
- «El péndulo simple no puede ser considerado como una medida del tiempo segura y uniforme, porque las oscilaciones amplias tardan más tiempo que las de menor amplitud; con ayuda de la geometría he encontrado un método, hasta ahora desconocido, de suspender el péndulo; pues he investigado la curvatura de una determinada curva que se presta admirablemente para lograr la deseada uniformidad. Una vez que hube aplicado esta forma de suspensión a los relojes, su marcha se hizo tan pareja y segura, que después de numerosas experiencias sobre la tierra y sobre el agua, es indudable que estos relojes ofrecen la mayor seguridad a la astronomía y a la navegación. La línea mencionada es la misma que describe en el aire un clavo sujeto a una rueda cuando ésta avanza girando; los matemáticos la denominan cicloide, y ha sido cuidadosamente estudiada porque posee muchas otras propiedades; pero yo la he estudiado por su aplicación a la medida del tiempo ya mencionada, que descubrí mientras la estudiaba con interés puramente científico, sin sospechar el resultado.»
-
- Christian HUYGENS: Horologium oscillatorium (1673).
Desarrollo teórico
La cicloide es la curva generada por un punto de una circunferencia que rueda sobre una línea recta. Si en un plano vertical construimos una trayectoria cicloidal, de base horizontal y con la concavidad dirigida hacia arriba, como se muestra en la Figura, tal trayectoria es tautócrona para el punto C; i.e., el tiempo que empleará una partícula P en resbalar (bajo la acción de la gravedad) hasta llegar a la posición de equilibrio estable C es independiente de la posición inicial de la partícula sobre la trayectoria cicloidal. Las oscilaciones alrededor de la posición de equilibrio son rigurosamente isócronas en una trayectoria cicloidal como la anteriormente descrita, y el periodo de las oscilaciones, que es independiente de la amplitud de las mismas, viene dado por
(1)
donde a es el radio de la circunferencia que genera la cicloide. Por consiguiente, el péndulo rigurosamente isócrono deberá ser tal que la masa pendular describa una trayectoria cicloidal.
Péndulo de Newton
El péndulo de Newton o cuna de Newton es un dispositivo que demuestra la conservación de la energía y de la cantidad de movimiento. Está constituido por un conjunto de péndulos idénticos (normalmente 5) colocados de tal modo que las bolas se encuentran perfectamente alineadas horizontalmente y justamente en contacto con sus adyacentes cuando están en reposo. Cada bola está suspendida de un marco por medio de dos hilos de igual longitud, inclinados al mismo ángulo en sentido contrario el uno con el otro. Esta disposición de los hilos de suspensión permite restringir el movimiento de las bolas en un mismo plano vertical.
El péndulo de Newton ha sido un popular juguete de escritorio desde su invención, nombrado y producido en 1967 por el actor inglés Simon Prebble. En un principio se vendía una versión en madera por Harrods de Londres y luego se diseñó una versión cromada creada por el escultor y luego director de cine Richard Loncraine.
El péndulo de Newton más grande del mundo fue diseñado por Chris Boden y es propiedad de The Geek Group y se encuentra en Kalamazoo, Michigan. Se encuentra en exhibición pública y es utilizado para demostraciones tecnológicas y científicas. Consiste en un conjunto de 20 esferas idénticas con un peso de 6,8 kilogramos (15 libras). Las esferas están suspendidas de cables de metal apuntalados al techo. Los cables poseen una longitud de 6,1 metros (20 pies) y las esferas cuelgan a 1 metro (3 pies) del suelo.
Péndulo de Pohl
El péndulo de Pohl es un péndulo de torsión constituido por un volante o disco metálico (v.g., cobre) que puede rotar alrededor de un eje y que, mediante un resorte espiral, recupera su posición de equilibrio, oscilando alrededor de ésta.
La idea original se debe al físico alemán Robert Wichard Pohl.
Péndulo simple
El péndulo simple (también llamado péndulo matemático o péndulo ideal) es un sistema idealizado constituido por una partícula de masa m que está suspendida de un punto fijo o mediante un hilo inextensible y sin peso. Naturalmente es imposible la realización práctica de un péndulo simple, pero si es accesible a la teoría.
El péndulo simple o matemático se denomina así en contraposición a los péndulos reales, compuestos o físicos, únicos que pueden construirse.
Ecuación del movimiento
Método de Newton
Consideremos un péndulo simple, como el representado en la Figura. Si desplazamos la partícula desde la posición de equilibrio hasta que el hilo forme un ángulo Θ con la vertical, y luego la abandonamos partiendo del reposo, el péndulo oscilará en un plano vertical bajo la acción de la gravedad. Las oscilaciones tendrán lugar entre las posiciones extremas Θ y -Θ, simétricas respecto a la vertical, a lo largo de un arco de circunferencia cuyo radio es la longitud,  , del hilo. El movimiento es periódico, pero no podemos asegurar que sea armónico.
, del hilo. El movimiento es periódico, pero no podemos asegurar que sea armónico.
Para determinar la naturaleza de las oscilaciones deberemos escribir la ecuación del movimiento de la partícula.
La partícula se mueve sobre un arco de circunferencia bajo la acción de dos fuerzas: su propio peso (mg) y la tensión del hilo (N), siendo la fuerza motriz la componente tangencial del peso. Aplicando la segunda ley de Newton obtenemos:
siendo at, la aceleración tangencial y donde hemos incluido el signo negativo para manifestar que la fuerza tangencial tiene siempre sentido opuesto al desplazamiento (fuerza recuperadora).
Al tratarse de un movimiento circular, podemos poner
siendo 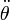 la aceleración angular, de modo que la ec. dif. del movimiento es:
la aceleración angular, de modo que la ec. dif. del movimiento es:
Esta ec. dif. no corresponde a un movimiento armónico simple (m.a.s.) debido a la presencia de la función seno, de modo que podemos asegurar que el movimiento del péndulo simple no es armónico simple, en general.
Método de Lagrange
El lagrangiano del sistema es
donde  es la elongación angular (ángulo que forma el hilo con la vertical) y
es la elongación angular (ángulo que forma el hilo con la vertical) y  es la longitud del hilo. Aplicando las ecuaciones de Lagrange se sigue
es la longitud del hilo. Aplicando las ecuaciones de Lagrange se sigue
y obtenemos la ecuación del movimiento es
de modo que la masa no interviene en el movimiento de un péndulo.
Recuperado de:
https://definicion.de/cascada/
https://es.wikipedia.org/wiki/P%C3%A9ndulo



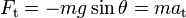
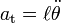




![T = 2 \pi \sqrt{\ell\over g}
\left[1+ \left(\frac{1}{2}\right)^2\sin^2 \frac{\varphi_0}{2}+
\left(\frac{1\cdot 3}{2\cdot 4}\right)^2\sin^4 \frac{\varphi_0}{2}+
\left(\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\right)^2\sin^6 \frac{\varphi_0}{2}+ \dots \right]](https://upload.wikimedia.org/math/6/6/b/66bbdb323cde9e38c8d33dfe5ff125bc.png)

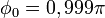 (negro), junto a un movimiento de pequeña amplitud
(negro), junto a un movimiento de pequeña amplitud 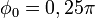 (gris).
(gris).